Entstehungshintergrund
|
Leonardo Fibonacci da Pisa (u.a. Leonardo Pisanus, Leonardus filius Bonacij – Kurzform Fibonacci) lebte von ca. 1180-1241 und gilt als der bedeutendste Mathematiker des Mittelalters. Durch seine vielen Reisen machte er sich mit Handelspraktiken (Währungssystemen) vertraut und studierte mathematische Relationen. Fibonacci Folge: 0+1=1 3+2=5 13+8=21 1+1=2 5+3=8 21+13=34 2+1=3 8+5=13 34+21=55… 0,1,1,2,3,5,8,13,21,34,55,89,144… Was ist nun besonders an dieser Zahlenfolge? |
 Leonardo Fibonacci da Pisa |
Euklid erwähnte erstmals um ca. 300 v.Chr. den Goldenen Schnitt. Er entdeckte spezielle Teilung von platonischen Körpern (Tetraeder, Hexaeder, Oktaeder…); die Pyramiden sind exakt nach dem Goldenen Schnitt konstruiert. Die katholische Kirche bezeichnete die Relation als „Göttliches Verhältnis“ und verwendete sie beim Kirchenbau (ähnlich der Griechen beim Tempelbau: Parthenon in Athen).
In der Natur ist ebenfalls dieser Goldene Winkel zu finden. Zwischen den aufeinander folgenden Blättern bzw. Samen entspricht der goldene Winkel exakt
= 360° – 360/1.618 = 137.503°
Dieses empfundene Schönheitsideal findet auch Beispiele in der Architektur, der Kunst, in der Musik und Astrologie (Venus-Uranus-Zirkel).
Die Fibonacci Zahlenfolge weist dieses „Goldene Verhältnis“ (Zahl Phi) auf, wobei n ein Element der Fibonacci Reihe ist:

Für die Technische Analyse werden nicht nur diese Zahl Phi, sondern auch deren linearen und quadratischen Verhältnisse genutzt. Ihre Berechnungen sind dabei wie folgt:
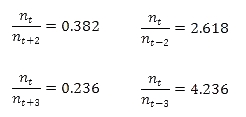
Für die quadratischen Verhältnisse ergibt sich:
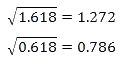
Anwendung Technische Analyse
Diese Fibonacci Verhältnisse können hilfreich bei der Kursanalyse sein. An der Börse kommt es zu immer wiederkehrenden Mustern. 1920 wurden die Fibonacci Zahlen im Bereich der Börse implementiert. Ralph Nelson Elliot erklärte in seinem Buch „Nature‘s Law“ die Fibonacci Verhältnisse zum Grundordnungsprinzip der Welt. Diese Muster von Kurskorrekturbewegungen können anhand der Fibonacci Verhältnisse berechnet werden. Läuft die Kurskorrektur in diesem Verhältnis zur vorrangegangenen Entwicklung so ist es wahrscheinlich, dass diese Gegenbewegung endet.
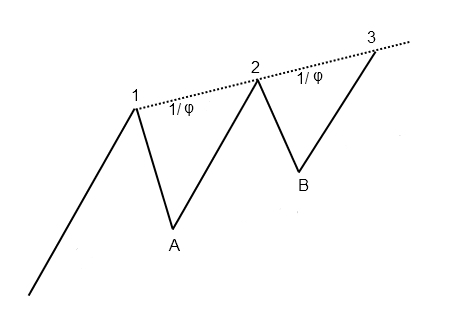
Three Drives to a Top
Die Abbildung zeigt eine stilisierte Kursbewegung. Die jeweiligen Hochpunkte (1,2,3) treten mit der vorherigen Gegenbewegung im Verhältnis 1/Phi auf. In den Punkten 1,2 und 3 könnten entsprechende Kerzenformationen (bspw. Shooting Star und Hanging Man) Verkauftssignale erzeugen. In der Praxis sind auch andere Fibonacci Relationen möglich, an denen eine mögliche Trendumkehr erfolgt.
Instrumente für die Technische Analyse
Fibonacci-Retracements
Diese Linien stellen horizontale Widerstands- und Unterstützungslinien dar, die aus dem Hoch- und Tiefpunkt der vorherigen Marktbewegung berechnet werden. Dadurch kann das Kurskorrekturpotential abgeleitet werden. An solchen Retracements erhöht sich die Wahrscheinlichkeit einer Umkehr.
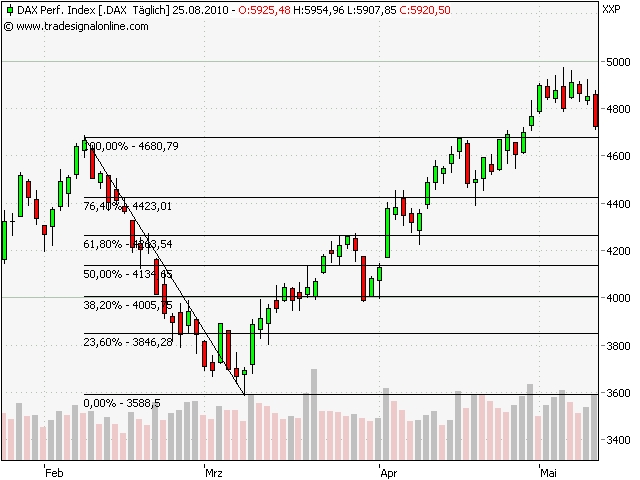
Fibonacci-Retracement
Die Abbildung veranschaulicht wie der Dax Index sich an den Fibonacci Retracements orientiert. An diesen Retracements erfolgten kurze Gegenbewegungen. Deutlich wird dabei, dass der Kurs nicht absolut drehen muss. Eine vorherige eindeutige Marktbewegung ist Voraussetzung für das Festlegen der Retracements.
Fibonacci-Zeitprojektionen
Bei dieser zeitraumbezogenen Analyse wird nach Wendepunkten im Kursverlauf gesucht. Hierfür kann der Abstand zwischen zwei Hoch- oder Tiefpunkten, aber auch zwischen einem Hoch- und Tiefpunkt untersucht werden. Die zeitliche Differenz zwischen zwei gewählten Zeitpunkten wird mit der Fibonacci-Sequenz multipliziert (0.382; 0.618; 1.618; 2.618). Der sich daraus ergebende Wert wird ausgehend vom Zeitraum als vertikale Linie abgetragen.
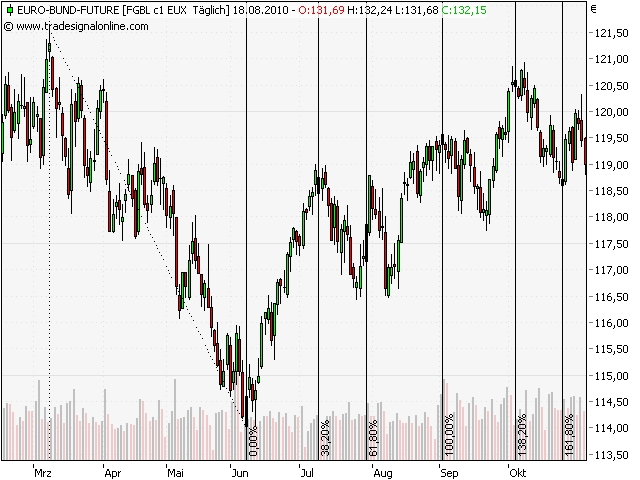
Fibonacci-Zeitprojektionen
Die zeitliche Differenz zwischen dem in der Abbildung gewählten Zeitraum (März – Juni) wird bei den Zeitprojektionen mit der Fibonacci Folge multipliziert. Es ist ersichtlich, dass mit hoher Wahrscheinlichkeit eine Trendwende an diesen Fibonacci Verhältnissen auftritt.
Fibonacci-Fächerlinien
Fibonacci-Fächerlinien werden an Hoch- und Tiefpunkten angelegt. Sie charakterisieren wichtige Widerstands- und Unterstützungsbereiche. Der wesentliche Vorteil bei Fächerlinien ist, dass Preis und Zeit gleichzeitig integriert werden. Quasi wie ein Retracement inklusive der Zeit.
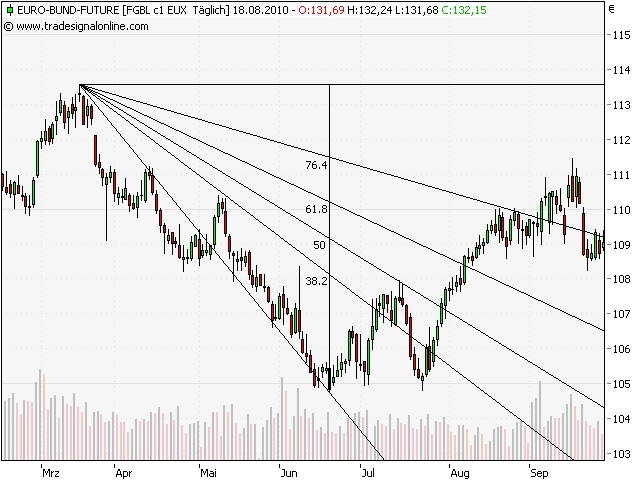
Fibonacci-Fanlines
Fibonacci-Extensions
Die Fibonacci-Extensions sind im Prinzip genau das selbe wie die Retracements. Die jeweiligen Preis-Linien werden hier allerdings über die angesetzte Welle hinaus gesetzt. So kommen Preis-Levels wie 127,2%, 161.8% oder 261.8% zustande. So sind diese auch hier für Wendpunkte relevant.
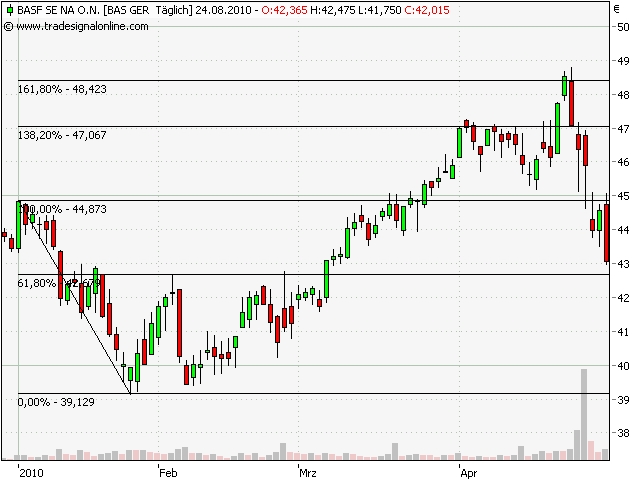
Fibonacci Extensions
Zunächst wurde vom lokalen Tiefpunkt (39€) und Hochpunkt (45€) eine Hilfslinie gezogen. Addiert man zu dieser Strecke die Fibonacci Verhältnisse von 38,2% und 61,8% erhält man die Extensions, hier: 138,2 % und 161,8%. Die Abbildung veranschaulicht wie der Kurs zunächst die 138,2% Extension erreicht und diese einige Perioden testet. Bei der signifikanten 161,8% Retracement kommt es zur Trendumkehr. Es sind auch weitere Fibonacci Hierachien relevant (127,2%, 138,2%, 261%, 423%).
Wir beschränken uns hier auf diese 4 Instrumente der Fibonacci-Analyse. Dies wird für unsere Analysen ausreichend sein.
Für weitere Fibonacci Instrumente wird auf die Literatur verwiesen.1
1 Vgl. Fischer R. (2001),The New Fibonacci Trader – Tools & Strategies for Trading Success; Fischer R./Fischer J. (2003), Candlesticks, Fibonacci, and Chart Pattern Trading Tools – A Synergistic Strategy to Enhance Profits and Reduce Risk